Применение современных методов математической статистики при проведении клинических исследований и их анализе. Cравнение двух пропорций

ВВЕДЕНИЕ

За последние 10–12 лет в теоретической и практической медицине произошли кардинальные изменения в области контроля за лекарственными средствами. В частности, появилось новое научное направление — доказательная медицина. Термин «доказательная медицина» (evidence-based medicine/EBM) впервые использовали в 90-х годах прошлого века Девид Саккет (David Lawrence Sackett) и его коллеги из Университета Мак-Мастера в Онтарио, Канада (McMaster University, Ontario, Canada).

Доказательная медицина своим происхождением во многом обязана работе Агентств по оценке новых медицинских технологий (Health Technology Assessment Agency), организованных в Великобритании, США, Канаде и ряде других стран. Большую роль в ее развитии сыграло Кокрановское сотрудничество — международная организация, которая занимается анализом рандомизированных клинических испытаний, и Агентства по оценке медицинских технологий, объединенные в международную сеть INAHTA (International Network of Agencies for Health Technology Assessment), а также центры доказательной медицины. Важное значение имеют центры доказательной медицины из большинства стран, в том числе России, где с декабря 2002 г. работает межрегиональное научное Общество специалистов доказательной медицины (ОСДМ), а в медицинских вузах созданы или создаются кафедры доказательной медицины.

Вместе с тем, необходимо помнить о том, что доказательная медицина не является догмой. В определенной мере доказательная медицина способствует деперсонализации и врача, и пациента, но ни в коем случае не отменяет личной ответственности врача за принятые решения. Схемы лечения, разработанные с помощью принципов доказательной медицины, могут служить основой для принятия решений, но не снимают с врача ответственности и не должны сужать возможности лечения.

Следует учитывать, что даже при проведении рандомизированных испытаний на самом высоком уровне их результаты имеют бесспорное отношение только к тем группам больных, которые участвовали в данном исследовании. Экстраполяция результатов исследований на конкретного больного может иметь свои существенные ограничения.

В настоящее время в Украине находят отражение международные интеграционные процессы в области разработки и обращения лекарственных средств (Good Laboratory Practice/GLP — Надлежащая лабораторная практика; Good Manufacturing Practice/GMP — Надлежащая производственная практика; Good Clinical Practice/GCP — Надлежащая клиническая практика; Good Distribution Practice/GDP — Надлежащая практика дистрибьюции лекарственных средств; Good Pharmacy Practice/GPP — Надлежащая аптечная практика). Вместе с тем, активная работа в области гармонизации международных стандартов GSP (Good Statistical Practice — Надлежащая статистическая практика) не проводилась. Внедрение вышеперечисленных стандартов, в частности GCP, без корректного применения статистических методов обработки данных, полученных в процессе исследований, практически не реально.

Прогресс доказательной медицины тесно связан с развитием современных информационных технологий и применением методов математической статистики.

СТАТИСТИЧЕСКАЯ ОБРАБОТКА КАЧЕСТВЕННЫХ ДАННЫХ.
СРАВНЕНИЕ ДВУХ ПРОПОРЦИЙ (ДОЛЕЙ)

В данной публикации затрагиваются вопросы статистической обработки качественных (нечисловых) данных¹ , в частности сравнение частоты проявления интересующего эффекта в двух группах (экспериментальной и контрольной).

При проведении анализа результатов клинического исследования часто возникает необходимость сравнить пропорции (доли) наличия или отсутствия какого-либо признака в двух группах, извлеченных из одной генеральной совокупности. Наличие или отсутствие интересующего признака является качественным показателем. Причем на разные группы влияли различные факторы или уровень их влияния был различный (лечение разными препаратами или одним препаратом в разных дозах). Например, в случае сравнения двух методов лечения (экспериментального и контрольного) можно сопоставить частоту возникновения нежелательных побочных реакций в экспериментальной и контрольной группах.

В табл. 1 приведен пример схемы составления таблицы, которая удобна для представления таких данных. В ячейках данной таблицы приведены обозначения, которые будут использованы в дальнейшем в формулах.

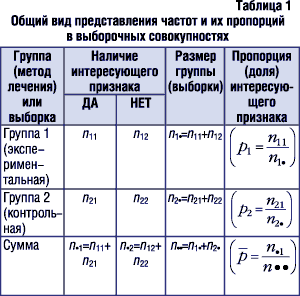Для того чтобы определить, являются ли различия частоты возникновения побочных реакций статистически значимыми, в качестве нулевой гипотезы (Н₀) выдвигается предположение, что пропорции P₁ и P₂ (истинные пропорции в генеральной совокупности) не различаются. Для определения достоверности различия пропорций P₁ и P₂ (с заданной доверительной вероятностью 100(1–a) %) можно применить z-критерий, критериальное значение которого рассчитывается по формуле:

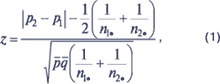где q=1–p, p₁ — выборочная оценка P₁, p₂ — выборочная оценка P₂.

Рассчитанное критериальное значение z сравнивается с процентной точкой стандартного нормального распределения² для уровня значимости³?a/2, так как данный критерий является двусторонним. Если вычисленное значение превышает критическое для заданного уровня значимости, то нулевая гипотеза отклоняется в пользу альтернативной, согласно которой пропорции P₁ и P₂ различаются с доверительной вероятностью 100(1–a)%.

Альтернативным вариантом, который приводит к тем же результатам, является сравнение квадрата вычисленного критериального значения (z²) с критическим значением функции распределения хи-квадрат с одной степенью свободы.

Кроме того, следует отметить, что включенное в формулу (1) выражение

является поправкой Иэйтса (Yates, 1934) на непрерывность. Это связано с тем, что непрерывное распределение (в нашем случае нормальное) используется для представления дискретного распределения частот. Поправку Иэйтса рекомендуется применять всегда, так как ее включение в формулу (1) приводит к более точной оценке сравнения вероятностей, чем в случае, когда поправка не используется.

Кроме того, можно вычислить достигнутый уровень значимости⁴?р (иногда его в литературе называют минимальным или наименьшим) и сравнить его с заданным уровнем значимости a. Традиционно полагают, если p<a, то этого достаточно, чтобы отклонить нулевую гипотезу на заданном уровне значимости a и принять альтернативную. Данная ситуация проиллюстрирована на рис. 1.

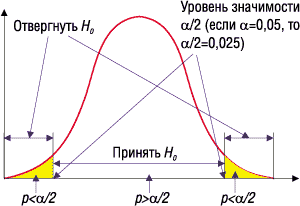Рис. 1. Иллюстрация применения p-значения

Если в результате использования z-критерия было установлено, что пропорции P₁ и P₂ различаются, то для их разности полезно построить доверительный интервал⁵ . Для его построения сначала необходимо вычислить оценку стандартной ошибки разности (p₂–p₁), используя следующую формулу:

где q₁=1–p₁ и q₂=1–p₂.

В случае, когда n_1• и n_2• достаточно велики (то есть n_i•p_i>5 и n_i•q_i>5 для i=1, 2), то 100(1–a) процентный доверительный интервал для разности P₂–P₁ определяется следующим выражением:

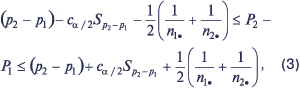где c_a/2 — процентная точка стандартного нормального распределения.

Построенный на основе выражения (3) интервал будет включать истинную разность пропорций приблизительно в 100(1–a)% случаев. Если доверительный интервал включает значение 0, то это свидетельствует о том, что пропорции P₁ и P₂ различаются статистически незначимо (при заданном уровне значимости).

ПРИМЕР

Сравним частоту возникновения нежелательных побочных реакций в экспериментальной и контрольной группах, исходные данные для которых приведены в табл. 2. Рядом с данными в скобках указаны обозначения, которые соответствуют используемым в вышеприведенных формулах.

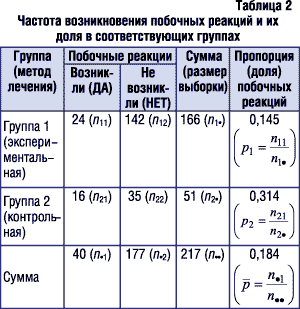Для расчетов воспользуемся электронными таблицами MS Excel. Вид исходных данных и полученных результатов на рабочем листе MS Excel приведен на рис. 2. Расчетные формулы рабочего листа Excel, которые запрограммированы в определенных ячейках, приведены на рис. 3.

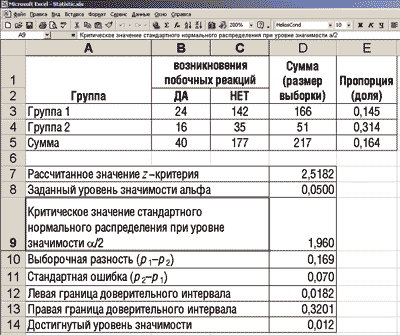Рис. 2. Исходные данные и результаты для сравнения долей и построения доверительного интервала их разности

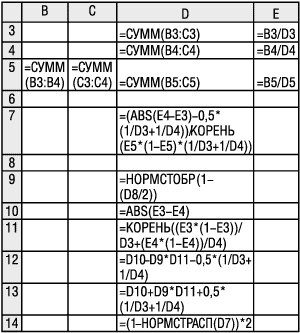Рис. 3. Формулы рабочего листа Excel для сравнения долей и построения доверительного интервала их разности

В соответствии с полученными результатами можно сделать следующие выводы:

1. Так как рассчитанное значение z-критерия (2,5182) больше критического значения стандартного нормального распределения при уровне значимости 0,05 (1,96) (при условии, что критерий двусторонний), то нулевая гипотеза отклоняется и принимается альтернативная, которая предполагает, что с доверительной вероятностью 95% пропорции P₁ и P₂ различаются. Другими словами, можно утверждать, что вероятность развития нежелательных побочных явлений/реакций при лечении пациентов первым методом статистически значимо меньшая, чем при лечении вторым методом.

2. Величина значения р, равная 0,012 (достигнутый уровень значимости меньше заданного уровня значимости a (a=0,05)), что также позволяет отвергнуть нулевую гипотезу в пользу альтернативной.

3. Стандартная ошибка разности оценок пропорций P₁ и P₂ равна 0,07.

4. Доверительный интервал для разности пропорций P₁ и P₂, полученный с использованием выражения (3), имеет следующий вид:

0,0182ЈP₂–P₁Ј0,3201.

Таким образом, можно утверждать, что истинная разность пропорций P₁ и P₂ приблизительно в 95% случаев будет попадать в данный доверительный интервал. Так как доверительный интервал не включает значение 0 при заданном уровне вероятности, то это также подтверждает сделанные в п. 1 выводы.

Несколько замечаний по поводу того, какой критерий — двусторонний или односторонний — следует выбирать.

Рассмотренный нами критерий, использующий стандартное нормальное распределение, является двусторонним. Он позволяет установить более значимое различие, если p₁ существенно больше p₂ или наоборот. Если же исследователь хочет проверить гипотезу, которая утверждает наличие различий только в одном направлении (например, что истинная пропорция во второй группе (P₂) больше истинной пропорции в первой группе (P₁)), то он может применить односторонний критерий, таким образом увеличив мощность такого исследования. Однако перед этим желательно изучить данные с целью поверки, насколько они согласуются с предположением односторонней гипотезы. Таким образом, односторонний критерий предусмотрен только для тех ситуаций, когда исследователя не интересует различие в направлении, противоположном тому, что утверждает гипотеза. Например, если альтернативная гипотеза состоит в том, что P₂>P₁, тогда для нас становятся безразличными другие альтернативы P₂=P₁ и P₂<P₁. Однако это редкость. В качестве одного из примеров такой ситуации, когда можно использовать односторонний критерий, может быть сравнение частоты возникновения побочных реакций в случае применения нового способа лечения (p₂) с частотой возникновения побочных реакций при использовании стандартного способа лечения (p₁), и новый способ заменит старый, если только p₂ значимо меньше, чем p₁. При этом не будет иметь значения, одинакова ли частота возникновения побочных явлений или же при новом лечении эта частота будет выше; и в том, и в другом случае исследователь будет применять стандартное лечение. В случае, если исследователь хочет, чтобы на результаты, полученные им, ориентировались его коллеги по профессии, то из этических соображений он должен выполнить проверки по двустороннему критерию. Если результаты свидетельствуют о том, что, например, частота побочных явлений при применении нового метода лечения выше, чем при применении стандартного (что можно выяснить только посредством двустороннего критерия), то исследователь обязан сообщить об этом с целью предупреждения тех, кто планирует изучение нового способа лечения.

В большинстве исследований применяется двусторонний критерий. Даже если все предыдущие результаты (теоретические выводы, данные предварительных исследований и т.д.) свидетельствуют о том, что наиболее вероятное различие будет только в одном направлении, исследователю лучше всего подстраховаться от возможных неожиданных результатов, применив двусторонний критерий. Различие, обнаруженное в противоположном направлении, с научной точки зрения является более важным, чем еще одно подтверждение различия в предполагаемом направлении.

Как проверить достоверность различий групп с использованием критерия хи-квадрат, а также вопросы, связанные с планированием исследований, формированием групп и др., будут рассмотрены в следующих публикациях.

А.В. Чубенко, Институт фармакологии
и токсикологии АМН Украины, Киев

Т.К. Ефимцева, Государственное предприятие
«Государственный фармакологический центр» МЗ Украины, Киев

¹ Качественные данные — данные, содержащие качественную характеристику определенного признака (например, давление: высокое, низкое, нормальное).

² Значение процентной точки берется из статистических таблиц (Большев Л.Н., Смирнов Н.В., 1983) или рассчитывается с использованием встроенной функции НОРМСТОБР(), как будет показано при рассмотрении примера.

³ Уровнем значимости называют максимально приемлемую вероятность отвергнуть нулевую гипотезу, если она верна (его называют также «альфа-уровень» и обозначают греческой буквой a). Другими словами, это максимальная вероятность совершить ошибку первого рода при проверке статистической гипотезы. Выбор величины уровня значимости a зависит от сопоставления потерь в случае ошибочных заключений в ту или иную сторону: чем весомее потери от ошибочного отклонения нулевой гипотезы, тем меньшей выбирается величина значения a. Обычно, на практике, значение a принимается равным 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Наиболее часто используется a=0,05, которое означает, что при пользовании определенным статистическим критерием, в среднем в пяти случаях из ста проверяемая статистическая гипотеза будет отклонена ошибочно.

⁴ Достигнутый уровень значимости (син.: р-значение, минимальный уровень значимости — это вероятность того, что значение критерия окажется не меньше критического значения при условии справедливости нулевой гипотезы об отсутствии различий между группами. Другими словами, p является вероятностью ошибочно отклонить нулевую гипотезу об отсутствии различий. Иногда говорят, что p — это вероятность справедливости нулевой гипотезы. Иногда в литературе достигнутый уровень значимости обозначается как P, хотя чаще всего достигнутый уровень значимости обозначается как p, а доверительная вероятность — как P. Здесь важно понимать смысл этих вероятностей исходя из контекста изложения.

⁵ Доверительный интервал — интервал, относительно которого с заданной вероятностью P=1–a можно утверждать, что он содержит неизвестное значение параметра q: P[q₁<q<q₂]=1–a, где 1–a — доверительная вероятность; a — уровень значимости. Таким образом, при помощи доверительного интервала можно оценить, в каких пределах с заданной доверительной вероятностью может находиться истинное значение параметра в генеральной совокупности. Например, значения параметров, полученные в результате проведения клинических испытаний на выборке, отличаются от истинных значений в генеральной совокупности вследствие влияния случайности. Так, 95% доверительный интервал означает, что истинное значение параметра, вычисленного на основе выборочных данных, с вероятностью 95% находится в пределах этого интервала. На основе доверительного интервала можно судить о клинической значимости эффекта. При помощи доверительных интервалов можно проверять статистические гипотезы. Например, для оценки статистической значимости различий существует следующее правило: если 100(1–a)-процентный доверительный интервал разности средних не содержит нуля, то различия статистически значимы (p<a) и, напротив, если этот интервал содержит ноль, то различия статистически незначимы (p>a).C Следует учитывать, что ширина доверительного интервала также характеризует степень нашего незнания: слишком широкий доверительный интервал может служить лишь указанием на то, что следует собрать больше данных. Доверительные интервалы дают больше информации о параметре, чем простая точечная оценка, поскольку отграничивают сразу целую совокупность допустимых значений.