Методология

Приведена последовательность действий, согласно которой сделан выбор метода для решения задачи о сравнении параметров распределения полученной выборки. Другими словами, описание разработанной методологии статистического анализа данных, полученных в ходе опроса 498 аптек-респондентов, а именно работников первого стола, в 25 региональных центрах Украины с развитой аптечной инфраструктурой.

Определение объема выборки

Чтобы получить достоверные результаты выборочных исследований, выборка должна быть однородной и репрезентативной. При выборке изучаемой совокупности факторов (ответы анкет), влияющих на рекомендацию определенного препарата провизором потребителю, не должно быть противоречий, изучаемая выборка должна быть репрезентативной (соответствующей) генеральной совокупности. В ходе исследования учтено общее количество фармацевтов-провизоров в Украине, составляющее более 30 тыс. человек, из которых около 20 тыс. человек — работники первого стола в областных центрах (согласно информации Государственного комитета статистики Украины (Госкомстата), 2002 г.). Для выяснения вопроса, сколько данных необходимо собрать, проведено установочное пилотное исследование. В ходе его определено необходимое количество аптек-респондентов при уровне достоверности полученных данных 95% (предельно допустимая ошибка d составила 5%).

Расчеты производили по формуле определения объема выборки при заданной абсолютной точности в оценке значений:

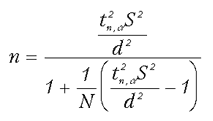где N — размер генеральной совокупности; d — абсолютное значение предельно допустимой ошибки в определении значения; S² — оценка выборочной дисперсии; t_n,a — для числа степеней n и уровня значимости a. Поскольку n точно не известно, для расчетов берут приближенное значение t_n,a? ~ 2.

Размер выборки сильно зависит от дисперсии, то есть от степени разброса данных — чем больше дисперсия, тем бoльшим должен быть размер выборки. Дисперсия постоянной величины равна 0. Если все результаты увеличить или уменьшить на одно и то же число, то дисперсия не изменится. Если все результаты изменить в К раз (например, с учетом коэффициента инфляции), то дисперсия изменится в К² раз (тот факт, что в период инфляции бедные становятся беднее, а богатые — богаче, с точки зрения статистики, является всего лишь свойством дисперсии). Корень квадратный из дисперсии представляет собой среднеквадратическое отклонение S (стандартное отклонение). С учетом вышеперечисленных свойств применена формула вычисления эмпирической дисперсии:

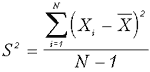Для обеспечения репрезентативности выборки генеральной совокупности (общее количество фармацевтов/провизоров первого стола) в каждом из исследуемых областных центров и согласно имеющемуся соотношению количества аптек к количеству населения (потенциальных потребителей) методом случайного отбора была определена экспертная группа (стратифицированная выборка). Эта выборка составила 498 аптек-респондентов, необходимых для получения достоверных данных.

Выбор метода статистического анализа

В связи с тем что при статистическом анализе использовали дискретную шкалу измерений, в дальнейшем было сочтено целесообразным применение непараметрического критерия в оценке полученных данных. Во всех случаях при использовании непараметрических критериев допускается следующее:

• все случайные величины взаимно независимы;

• анализируемые выборки распределены по непрерывному распределению одного и того же вида.

В данном исследовании проверяли гипотезу о равенстве не среднего, а медианного значения. Это связано с тем, что для закона распределения, отличного от нормального (измерение в дискретных шкалах), медиана является более устойчивой и корректной оценкой положения центра распределения. Определение медианного значения всей выборки (по всем заданным вопросам) производили для определения значимости каждого фактора, исходя из полученных ответов респондентов (см. рис. 1).

Полученные обобщенные данные определения медианы с учетом дисперсии и предельно допустимой ошибки приведены в табл. 1.

Определение медианы с учетом дисперсии и предельно допустимой ошибки

Определение взаимосвязи между существующими факторами

Следующий шаг в исследовании был направлен на определение взаимосвязи между всеми существующими факторами (определение корреляционной последовательности) методом ранжирования вариационного ряда и вычислением коэффициента корреляции методом Спирмена. Медиана (выборочная) — это значение, которое делит ранжированный вариационный ряд на равные по объему группы.

Вариационным рядом называют значения случайной выборки (x₁, x₂, …x_n), имеющие функцию распределения F(x) и расположенные в порядке их возрастания: x₍₁₎ < x₍₂₎ < … < x_(i) < … < x_(n), где i-й член вариационного ряда x_(i) называют i-той порядковой статистикой, а номер члена вариационного ряда — рангом, порядком статистики. Ранжирование — это процедура перехода от совокупности наблюдений к последовательности их рангов.

В нашем случае необходимо проверить, существует ли статистически значимая связь (зависимость) между заданными факторами, которые являются параметрами в формировании мнения работника первого стола и в дальнейшей рекомендации им потребителю того или иного препарата. Для этого имеющиеся значения переменных размещают в ранжированном (упорядоченном по величине) ряде (см. рис. 1). Затем каждому значению присваивается ранг от 1 до N, где N — количество анализируемых объектов (в нашем случае от Ф1 до Ф15). Так как несколько элементов в исследуемой выборке имеют один и тот же ранг, то каждому из них присваивается среднее значение (средний ранг). Совокупность элементов выборки, имеющих одинаковое значение, называют связкой, а количество одинаковых значений — ее размером. Поскольку в исследовании рассмотрены субъективные оценки объективных явлений, то есть экспертные оценки, а закон распределения изучаемых переменных не является нормальным, то одним из способов статистического анализа данной выборки является определение коэффициента корреляции Спирмена (табл. 2).

Коэффициент корреляции Спирмена вычисляется по формуле:

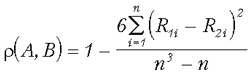где R_1i и R_2i — ранги i-того объекта для каждой из сравниваемых переменных.

С учетом наличия совпадающих значений (связок) знаменатель уменьшается на величину:

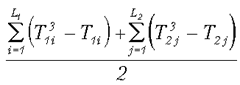где L₁ и L₂ — количество связок в T_1i и T_2j — размеры связок (количество элементов в них).

Таблица 2

Ранговая корреляция (метод Спирмена)

* Полужирным шрифтом выделены наиболее значимые корреляционные взаимосвязи между исследуемыми параметрами, влияющими на формирование мнения работника первого стола.

** В экспертном анализе использовались показатели со значением r > 0,25 (в таблице — курсив).

Определение значимости исследуемой выборки

Поскольку проводили анализ случайных величин, одной величины коэффициента корреляции для вывода недостаточно. Необходимо было проверить, значимо ли он отличается от нуля. Статистическую значимость корреляции исследуемых факторов проверяли с помощью критерия Стьюдента. Фактически проверяли гипотезу о равенстве коэффициента корреляции нулю. Для этого рассчитывали критериальное значение по формуле:

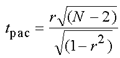где r — значение коэффициента корреляции, а N — количество наблюдений.

Для подтверждения значимости коэффициента корреляции необходимо сравнить t_рас и t_таб (табличное значение распределения Стьюдента обратное). Если расчетное значение t (t_рас) больше табличного, взятого с N –2 степенями свободы, то нулевая гипотеза отвергается. Это означает, что коэффициент корреляции значимо отличается от нуля (с выбранным уровнем значимости). Результаты проведенного статистического сравнения (табл. 3) доказывают значимость корреляционной связи для каждого исследуемого фактора отдельно и в общем.

Таблица 3

Значимость коэффициентов корреляции (“+” значимо, “-” не значимо) при сравнении с t_таб =2,048 (правомерной для данной выборки)

Результаты данного статистического анализа выборки (498 аптек-респондентов в 25 региональных центрах Украины), составившей по отношению к генеральной совокупности до 20 тыс. фармацевтов и провизоров первого стола, свидетельствуют (с достоверностью до 95%), что выборка репрезентативна генеральной совокупности и достаточно отражает структуру генеральной совокупности (по данным Госкомстата, в Украине на 2001 г. число фармацевтов и провизоров составило около 35 тыс. человек). Другими словами, влияние выбранных для исследования факторов и их взаимосвязи, позволяет с бoльшей достоверностью оценить (экспертная оценка), за счет каких моментов формируется мнение фармацевта/провизора в его рекомендации потребителю того или иного препарата.